© Matthias S. Benkmann <article (a) winterdrache.de>
Computer animation can be a useful tool when teaching algorithms. When designing algorithm animations, several factors have to be taken into account to make sure the result is educationally effective. Among the aspects that have to be considered are the scope of the animation, the level of abstraction, the visual presentation of data and the kind of interactivity features to be offered. After discussing these general issues that apply to most algorithm animations, this paper introduces PRPVis, a program that visualizes the Probabilistic Roadmap Planner (PRP). The PRP is a motion-planning method that can be used for, among other things, finding paths for moving a robot through an obstacle course. With this use-case as the basis for the visual presentation PRPVis offers interactive demonstration and exploration of the PRP's core algorithm. PRPVis can be used as a demonstration aid in a lecture but is also suitable for interactive use by students as part of homework or guided lab sessions. This paper explores these possibilities and presents several example exercises that demonstrate the use of PRPVis as part of a course.
Algorithms are one of the most important parts of computer science. At the same time they can be among the most difficult to learn and teach. A major reason for this difficulty is that algorithms are dynamic in nature. While you can write down an algorithm as static pseudocode, unlike a narrative text it can not be understood just by reading it through sequentially, unless it is extremely simple. In order to understand an algorithm, you have to develop a mental model of its dynamic behaviour. In theory it is possible to do this from pseudocode alone, by executing the algorithm by hand for different sets of example data, but in general this method is unfeasible and is very inappropriate for teaching.
This raises the question how an algorithm can be communicated effectively to students, i.e. how its dynamic behaviour can be presented adequately. The natural answer is visualization, the use pictures to show what is otherwise hard to explain by words alone. Pictures are one of the oldest methods of human communication and at the same time one of the most universal and effective. However, just like text a picture is static, so to describe the dynamics of an algorithm, one picture is not enough. When textbooks use pictures to explain an algorithm, they usually depict several snapshots of an example of its execution. The number of such snapshots is severely limited by the space constraints of printed media, so the presentation is often unsatisfactory due to its incompleteness. The logical step to overcome this limitation is to employ more dynamic media, such as film, to go from pictures to animation. This leads to the field of algorithm animation.
Although the basic idea of using animation to visualize an algorithm is simple and obvious, developing algorithm animations that are effective as teaching aids is a challenging task. It begins with the choice of medium, since there are several ways to present animation. As they become more and more widespread and in general have very powerful graphics capabilities today, computers have become the medium of choice for many kinds of educational applications. Computer-Assisted Instruction (CAI) has been gaining in popularity in recent years and it is to be expected that this trend will continue. For algorithm animation as part of computer science education the computer is certainly the most natural medium and for the rest of this text "animation" will always refer to animation on a computer.
Once the medium has been chosen, the animation itself must be designed and developed. Although there are a lot of guidelines and considerations that apply to algorithm animation in general, an educationally effective animation needs to be specifically tailored to a given algorithm. The first part of this paper will discuss those issues that apply to algorithm animation and visualization in general. The second part will pick up these issues and put them in a concrete context, namely the PRPVis program, an interactive visualization for the Probabilistic Roadmap Planner. The presentation of PRPVis is complemented by the third part which gives examples for how PRPVis can be used in a course setting.
As already mentioned in the introduction, animation is a very natural thing to be used for teaching something dynamic such as an algorithm. However, this is not the only justification for algorithm animation. One aspect whose importance must not be underestimated is student motivation. As studies such as [1], [2] and [3] and many others have shown, animations are generally well-received and appreciated by students, regardless of any measurable improvement in learning effectiveness. And as practically anyone who has ever studied something will attest, motivation is a key ingredient to a good learning experience. Although often marginalized in quantitative studies that are concerned mainly with the comparison of pre-test and post-test scores, psychological factors such as enthusiasm and enjoyment play a major role in any learning environment. For instance, working with students that are interested in and enjoy working on the subject matter is much easier and less stressful for the instructor than preaching against a wall of impassive ignorance.
Especially in the private sector the learning atmosphere is directly related to "customer satisfaction" and consequently is a major concern that influences the economic success of a private educational institution. "Edutainment", the fusion of "education" and "entertainment", is one of the buzzwords that have appeared in recent years in the field of education. There is a growing market for computer software that entertains while it teaches. It can be expected that future generations of students, who have grown up with computer games and multimedia on the WWW, will come to demand more than just blackboard and textbook courses, and will make this a factor in their choice of educational institution.
Speaking of computer games and multimedia, this leads to another, so far unmentioned, advantage that animation has over static text or pictures. This advantage is interactivity. While it is possible to introduce interactivity into text and pictures, it is together with animation that interactivity is most powerful and satisfying for the user. Often the desire for interactivity is what motivates the creation and/or use of teaching software in favour of more traditional media such as textbooks. Animation is then often just a natural consequence of making the interactive interface useful and visually pleasing. This strong focus on interactivity can be detrimental to the educational value, however. At least with respect to algorithm animation, interactivity can be a double-edged sword, as described in [2], namely when it tempts students to mimic the steps of the algorithm without leading to true comprehension.
Someone with a deep understanding of an algorithm can usually design an appropriate animation intuitively. In fact, most algorithm animations probably start out as ad hoc implementations rather than as the result of a formalized development process. Although these programs are often very impressive and useful, there comes the point when further development requires formal criteria based on which the application can be evaluated and improved. The following sections will present such criteria and later on the PRPVis program will be examined with respect to the points discussed here.
There are many different issues the designer of an algorithm animation faces. When trying to approach the task of developing or improving an algorithm animation systematically, it is useful to isolate, name and define the most important aspects, so that they can be discussed, evaluated and designed with a clear focus. In [4] Roman and Cox have developed a taxonomy of program visualization systems that can serve as a useful framework for discussing the important aspects of an algorithm animation system. The following classification is similar, but with the focus on the development of standalone algorithm animations such as PRPVis, rather than general program visualization systems. Some of these aspects will be examined more closely in the upcoming sections.
The question that is usually at the beginning of an algorithm visualization project is "What parts of the algorithm are to be visualized?". An algorithm can be characterized by its code, its data, its control state and its execution behaviour. Furthermore, algorithms often don't work in isolation. There may be other algorithms employed for subtasks or preparation, for example. Although it is usually among the first to be worked out, the scope aspect is not only important at the beginning of a project. It has to be watched closely throughout the development process, because developers have the tendency to add more and more features as an application matures, and an animation that is too broad in scope, just like one that is too narrow in scope, is diminished in its educational effectiveness.
This aspect deals with the relationship of the visual representation to the underlying algorithm, especially how closely the two are related. Pseudocode for instance offers a very low level of abstraction; it is very close to the algorithm. Algorithm animation applications often have several views that present the underlying information at different levels of abstraction. Although the range of possible abstractions is continuous, there are a few ways of representing information that are conceptually distinct enough to be named and discussed in more detail. These are direct, structural, synthesized and explanatory representation.
A major difference between the computer and most other media is that the computer permits sophisticated interactivity. Interactivity comprises all the means that the user has to influence what is displayed by the computer. The proper use of interactivity can improve a visualization significantly, whereas improper use can diminish the educational value. Interactivity can serve different purposes in algorithm animation programs and consequently different kinds of interactivity can be distinguished. In this paper three different types of interactivity will be discussed: playback control, tests and creative interaction.
Because the information contained in an algorithm and its execution is non-physical, it can be presented in different ways. Even data that has a very close connection to the real world, such as 2-dimensional coordinates, can be displayed in a multitude of ways. The presentation aspect covers all the design choices made with respect to the actual displaying of the information on the screen. It deals with questions such as "How can colour be used to help the user understand the animation?" and "Which views should be visible at the same time?"
This paper discusses algorithm animation as a teaching tool, so the purpose of the animation in this context is to help the viewer understand the algorithm. Although communicating a complete and perfect understanding of the algorithm to the student would be very desirable, it is impossible to achieve, because there are too many facets to an algorithm, such as its runtime behaviour, big-O complexity, use-cases, optimizations, variants, and so on. One peculiarity of human learning behaviour is that when too much information is presented all at once, the result is under most circumstances a reduced learning effectiveness. Furthermore, developing a visualization that covers every single aspect of an algorithm, if that is at all possible, would require an impractical amount of time and development resources. So clearly when designing an algorithm animation, it is necessary to carefully think about its scope, i.e. what aspects of the algorithm it should cover.
Despite there being a long list of aspects of an algorithm that could be covered, general algorithms education focuses on a small set of core aspects. Of those listed in the preceding paragraph, optimizations are one aspect that is often omitted, for instance. In the context of visualization even fewer aspects are of interest. Big-O complexity, for example, is usually not a topic that is explicitly included in algorithm animations (although it may be visible as a side-effect). In the following, some of the more important facets of an algorithm that are often within the scope of algorithm animations are presented.
When algorithms are taught, it is usually to enable the students to implement them, so actual code or pseudocode that demonstrates the algorithm's implementation is normally part of any presentation of the algorithm. Furthermore, printing code is one of the most primitive and easy to implement forms of visualization, so the cost of including it in the program is very low. Code does not need to be presented as text, though. Depending on its complexity and organization, other forms of visual code representation such as diagrams in the Unified Modeling Language (see [5]) may be preferable, especially when the code is to be part of an animation.
The control state describes aspects such as which statement of the code is currently being executed or is to be executed next. Other aspects of the control state may include which conditional statements are true, which branches will be taken, how often a loop has been executed and so on. The control state is usually very low-level information and to a large degree out of scope for many animations. The most notable exception is an indicator for the currently active statement. When the code is included in the animation, such an indicator is a natural addition.
Most interesting algorithms process data, often contained in sophisticated data structures. That some visual representation of the data is contained in the animation is almost inevitable if the animation is to be useful, however it is an important question whether the data and especially the data structures are to be animated only as necessary to demonstrate the algorithm, or whether they should play a significant part in the visualization. When animating the HeapSort sorting algorithm, for example, it must be decided whether a visualization of the heap structure is to be part of the animation or not. The decision whether the data aspects are in scope for the animation to be designed often depends on the larger context in which the animation will be used. If the HeapSort animation is to be part of a comparison of different sorting algorithms, animated side by side, then visualizing the heap structure would be confusing, as it has no counterpart in other sorting algorithms, such as BubbleSort. If, on the other hand, the HeapSort animation is presented together with other algorithms that operate on heaps, the heap structure deserves special attention.
The execution behaviour of an algorithm refers to the changes that data, control state and possibly code go through while the algorithm is executing. The execution behaviour of an algorithm is normally in scope for an animation of that algorithm, except for very unusual cases, such as an animation that morphs a representation of the algorithm's code into a different representation, e.g. to visualize a certain optimization of the code. The more difficult decision is how much of the algorithm's execution behaviour should be covered by the animation. As has been mentioned, too much information can overwhelm the viewer, so the choice has to be made carefully. One of the more important questions in this context is whether the animation should only ever show one state of the system, presenting execution behaviour only through the animated changes of state, or whether past states, i.e. the execution history, should be visible, too.
Most algorithms are modular in at least one of two ways. The more common way is for the algorithm to be a module of a larger system. A sorting algorithm for instance is normally included as one component of a larger application, rather than being the dominating part of the program. But modularity in the other direction is also possible. Some algorithms contain subtasks for which they employ other algorithms that are independent. The Probabilistic Roadmap Planner for example requires an algorithm to find a connection between two nodes within a graph. This could be the well-known Dijkstra algorithm, but any other algorithm such as A* (see [6]) could be used instead. It is clear that this is not an actual part of PRP. When designing an algorithm animation, it must be decided, if the modularity aspects are within or outside of the scope envisioned for the animation. If the decision is made that they should be included, there are many different techniques that can be employed to animate them, such as dynamic expanding and folding of the sub-algorithm's code.
When you are surrounded by trees you cannot see the forest as a whole. But if you fly inside a helicopter to get a bird's-eye view, you will see the forest just fine. The individual trees, however, will be difficult to make out. This metaphor describes the heart of abstraction, namely presenting views that can be closer to or farther away from the original information that is to be conveyed. Abstraction is an important aspect of algorithm animation, because well-chosen abstractions can be extremely helpful to the viewer, as they can concentrate the focus on certain aspects, emphasizing them while other details move into the background.
Let's take an animation of QuickSort as an example. Common visualizations depict the elements of the array to be sorted as horizontal or vertical bars whose length corresponds to the element value (see for instace [7]). It can be useful, however, to present a view in which elements are not marked according to their actual value in any way, but simply distinguished based on whether they are greater than or less than the pivot element. This abstraction loses some information compared to the view with the bars of different sizes, but in exchange for this loss, one of the algorithm's core aspects is more clearly visible, namely that elements are reordered so that all elements greater than the pivot end up on one side of the pivot and those smaller than the pivot end up on the other side.
The range of possible abstractions is continuous, but the following four categories of representations (based on the categorization in [8]) are reasonably distinct to warrant closer examination. They are ordered by increasing level of abstraction.
The above-mentioned common way of visualizing sorting algorithms by presenting the array to be sorted as a sequence of vertical bars, whose heights correspond to the values of the array elements the bars represent, is an example of the simplest form of representing information. It is a more or less injective mapping of the numerical data to pictures. The graphical representation basically allows reconstructing the original numerical data. So it is a direct representation of the underlying data, the lowest level of abstraction possible. While direct representations can be useful, they are usually not enough on their own in the context of education.
Very often, especially in educational settings, there are certain higher level aspects of an algorithm that should be emphasized due to their importance. In the example of QuickSort, the reordering of the elements relative to the pivot element, based only on the less-than/greater-than relation and not the actual value, is such an important aspect that must be communicated when teaching QuickSort. The presentation of higher-level structural aspects such as this is only hindered by the details contained in a direct representation. A structural representation remedies this problem by eliminating some of the detail information from the direct mapping, in order to make the interesting structural aspects more pronounced. This achieves a higher level of abstraction.
While the structural representations just discussed are still based on direct representations, merely removing some details and emphasizing others, synthesized representations actually add something new. A synthesized representation shows something that has no direct counterpart in the underlying algorithm or its data. It presents new information that is derived from the information directly contained in the algorithm or its data.
This is a major step up on the abstraction ladder and also often increases the complexity of the implementation, because it can become necessary to add new code and data structures closely tied to the underlying algorithm, in addition to the graphics code that is always required for a visualization. This increases the maintenance burden, because it must be avoided that the core algorithm and the synthesized representation get out of sync.
As an example consider an animation that demonstrates insertion of points into an R-tree. If the animation simply plots the points stored in the R-tree and the organizing rectangles, as well as how they grow with more points being inserted, this is direct representation. It might be desirable, however, to draw areas where multiple rectangles overlap in a different color to emphasize the degradation of the tree. Unfortunately this information is not contained directly within the tree data. But the overlapping regions can be synthesized by computing the intersections of the rectangles stored in the tree.
Direct representation, which shows the information as it really exists, is the lowest form of abstraction. Explanatory representation is at the other extreme. Like a synthesized representation, an explanatory representation shows something that is not found directly in the algorithm or its data. The line between synthesized and explanatory representation is hard to draw, but conceptually explanatory representation works on a higher level of abstraction, because it is concerned not so much with the actual information about the algorithm but rather with meta-information, i.e. information about the information.
The distinction is mainly one of intent. Explanatory representation refers to those parts of the visualization that have been added not because they show a part of the underlying algorithm or are derived from it in a natural way, but rather because they serve to make the visualization easier to understand or more aesthetically pleasing.
Take the QuickSort example again, where every element of the array being sorted is represented by a vertical bar of length proportional to the element's value (direct representation). The pivot element could be represented by a bar that blinks. While the pivot element's bar is by itself a direct representation, the blinking feature is an example for explanatory representation. While the blinking does represent information that is part of the algorithm's execution, namely which element is the current pivot, it is not really derived from that information. After all, blinking is a quick alternation between two states, but no such state changes occur on the pivot during QuickSort. Furthermore, the blinking modifies the visual appearance of the pivot element's bar, which is after all its direct representation. Inside the algorithm, however, the pivot element remains unmodified. The blinking is merely a visual cue that helps explain the inner workings of QuickSort.
Explanatory representations can be very helpful, but they can also be misleading. In the above example a naïve viewer might be tempted to believe that QuickSort does in fact modify the pivot element to mark it in some way. After all, in a different context it would not be unusual to use blinking to signify that an element of an array is currently being modified.
The desire to implement interactive features in computer programs is strong. They are often seen as one of the major advantages computers offer over textbooks or non-interactive video films. The benefits of interactivity seem intuitively clear and interactivity is also very popular among and considered beneficial by students as can be seen from their comments in studies such as those presented in [2]. But subjective perception and intuition can be misleading. The results from the studies in [2] demonstrate that the value of interactivity in algorithm animation programs rises and falls with its proper use by the students. Especially the fact that students like the interactive features, while appearing to be a benefit at first glance, turns out to be quite problematic. It causes students to spend more time with the program, but this additional time spent does not necessarily translate to a better understanding of the subject matter. It appears that for some students, mostly the weaker ones, the interactive features transform the program into some kind of video game. They play around with it but do not gain deep insight into the algorithm presented.
In spite of these negative results, interactivity is not generally harmful or irrelevant. In the studies mentioned above the better students seemed to benefit from the interactivity, which suggests that the key to success with respect to interactive features lies in the proper and disciplined use of them. It is therefore imperative that interactive features planned for an algorithm animation be examined carefully to make sure that they do not encourage undirected and mindless playing around. If possible, the program should guide the use of interactive features that could be problematic. Classifying interactivity features into different categories can aid in deciding what features should be implemented and what other features are better left out or need special consideration with regards to detrimental effects they could have. The following is such a classification that can be helpful when considering these issues.
The most primitive and obvious form of interactivity, to be found in almost all algorithm animation applications, is playback control. Playback control features allow the viewer to control the playback of the animation, but not its contents. The most common features in this class are play, pause and restart. Playback speed is also often under the control of the user, usually including a single-step mode that permits viewing the animation in small steps, sometimes frame by frame. Less frequently encountered, because it is difficult to implement, is reverse execution which allows the viewer to view the animation backwards, i.e. execute the algorithm in reverse. This feature can be very useful to back up and take another look at some steps.
The usefulness of playback control is undisputed. Every algorithm animation should have at least the basic play, pause and restart controls. For features beyond these the case is not so clear. A single-step mode is a useful addition under most circumstances, but whether the benefits, if any, of more complex features, such as backwards execution, justify the added implementation and maintenance work, requires more consideration. Regarding detrimental effects on the learning value of the program, playback control features are relatively safe. They may end up unused but under normal circumstances they won't hurt the user experience.
A form of interactivity that is found in many educational programs are tests that present questions about the subject matter that the student has to answer. The tests are often multiple-choice or require typing in answers that consist of only a single unambiguous word or number. There are more complex forms of tests, however, especially in the context of algorithm animation. The student could be required, for instance, to perform certain steps of the algorithm by dragging around with the mouse some graphical objects that are part of the visualization. Normally these tests exist only to give the learner instant feedback about how well he has understood the concepts presented in the program, but given the proper infrastructure for transmitting the answers, they can also be used as homework that is handed in and graded.
Tests are an issue of constant debate among educators. Especially test methodologies such as multiple-choice have been criticized as too simplistic and are accused of encouraging the wrong learning styles. But even more sophisticated tests can lead to ineffective, even counterproductive learning behaviour in students. The studies presented in [2] used an algorithm animation courseware to teach binary trees, graphs and sorting. The system included an "I'll try" mode, using which students could attempt to perform steps of the algorithm themselves and were given instant feedback on the correctness of their actions. Some students used this mode too soon, wasting much of their time guessing answers, possibly learning to produce the desired results without any real understanding of the algorithm.
As [9] demonstrates, it is possible for a human to learn even complex processes on a purely visual basis, without ever understanding the underlying principles. Tests that provide instant correctness feedback and that can be tried over and over again may trigger this kind of learning, especially in a visual environment such as an algorithm animation. But in most cases this kind of visual trial-and-error learning is superficial and undesirable, because the knowledge gained in this way is incomplete, and when faced with problems that go beyond executing the algorithm by hand, students will generally fail to succeed when all they have learned is to mimic the steps of the algorithm's animation.
To be an improvement rather than a burden, tests integrated into educational software must be wisely chosen. The restrictions with regard to the medium, such as the desire to have automated evaluation, must be considered, as well as bad learning styles that the tests could encourage. The HalVis system presented in [10] includes an interesting feature that demonstrates beneficial use of tests. HalVis occasionally presents the user with so-called "tickler" questions. These questions serve to make the user test his own knowledge and become aware of issues that he might want to explore further. This is an unconventional approach to computer-implemented tests, because the computer presents only the question and the means to figure out the answer, but it does not actually receive and evaluate the user's answer. The main disadvantage of this approach is that it relies on the user's ability to judge his own understanding, but in exchange for this, many other problems associated with tests are easily avoided.
The behaviour of most algorithms depends on the data they operate on. Furthermore, many algorithms have special cases, i.e. pieces of the algorithm's code that are only executed when the input data has certain properties. To be able to interactively explore all of these cases, the viewer must be allowed to provide his own data to the algorithm. This is the essence of creative interaction. The viewer effectively creates his own animation of the algorithm within the constraints set by the animation program.
The study described in [11] shows how beneficial active experimentation can be. Students who participated in the active lab sessions, where they explored the workings of an algorithm on data they entered themselves, performed significantly better than students who did not have this opportunity. The desire of the students to be able to construct their own input data is also apparent from the think-aloud protocol recorded as part of the study described in [2].
These results are not surprising. Even if the provided animations of the algorithm cover all of its special cases, and even if the viewer has understood the animations, the viewer may not comprehend the algorithm completely. The choice of data to demonstrate the algorithm with, that seemed appropriate to the person creating the algorithm animation, might not be the best choice for every viewer. Furthermore, some people need to view several different examples of the same concept in order to understand it. The ability to create their own examples can be of much help to viewers.
Especially when the algorithm being animated has many different cases, creative interaction features can allow the student to resolve all the uncertainties that the preconfigured animations may have left. Creative interaction also encourages thinking actively about the algorithm, especially its difficult parts. This makes creative interaction very desirable to have when animating algorithms whose behaviour varies greatly for different sets of input data. However, care must be taken to make sure that the students use the provided features properly, i.e. to clarify questions about the algorithm's behaviour. It must be prevented that students play around with the features simply to create animations that are aesthetically pleasing, funny or otherwise interesting without being educational.
The Probabilistic Roadmap Planner (PRP) is a motion planning method that can for instance be used to find a path for moving a robot through an obstacle course. As the name implies, PRP is a roadmap-based approach. The heart of PRP is a probabilistic algorithm that constructs a roadmap graph that describes movements the robot can perform without colliding with an obstacle. PRPVis is an interactive animated visualization for learning about and exploring the core concepts of PRP. Before the PRPVis program is described in detail, a short introduction to PRP as it is implemented in PRPVis will be given. For a more detailed introduction see for example [12].
The following terms will be used througout the descriptions of PRP and PRPVis.
To make the description of PRP easier to read and understand, it will be assumed that it is being used to plan the movement of a robot, although PRP is a general method that plans transitions between multi-dimensional states that could describe anything. So the term robot is used to refer to the entity whose state transitions are being planned.
The different kinds of movements that the robot can perform, such as move forward, move backward, rotate clockwise around an axis, etc. are called the robot's degrees of freedom(dof).
The configuration space is the set of all possible states, called configurations, that the robot can assume. The configuration space depends on the robot's dof, but it is not uniquely determined by them, since there are different ways of describing the states for most robots. For car-like robots the configuration space is often chosen as a multi-dimensional vector space that has coordinates which describe the robot's location and orientation.
The free space is the subset of the configuration space that contains all points that correspond to states that the robot may assume without violating any constraints placed on its movement.
An obstacle is a subset of the configuration space that contains points that correspond to states that the robot must not assume, e.g. because the location part of the state is within a solid physical wall. When a physical setting is discussed, it makes sense to speak of several obstacles but in a more abstract situation the term "obstacle" often refers to the complete subset of illegal states, so that there is exactly one obstacle, defined as the complement of the free space within the configuration space.
An algorithm is probabilistic if it is based on probability and statistics. A probabilistic algorithm contains a random element as a major influence on the results.
A roadmap is a directed graph. Its nodes correspond to points in the free space. An edge from node A to node B signifies that the robot can make a transition from the state corresponding to A to the state corresponding to B, without having to assume any illegal intermediate states. In the common case of moving a robot through a physical obstacle course, an edge in the roadmap could mean that the robot can move from point A to point B without hitting a wall. A roadmap usually covers only a very small subset of the free space and possible state transitions, but does not contain information on how to perform the actual transitions, only that they are possible.
A path is an ordered sequence of points in the free space with the property that the transition between a point in the path and its successor is possible for the robot without having to assume any illegal intermediate states. A path "within a roadmap" is a path whose points are all represented as nodes in the roadmap, with an existing edge from each point to its successor in the path.
A planner is a method to find a path from point A to point B. A global planner is a planner that is prepared to plan paths from any point in the free space to any other, even if the two points are very distant (by whatever notion of distance applicable) and obstacles have to be evaded. A local planner is a planner specialized for planning paths between points in the free space that are close (by whatever notion of distance applicable). Often local planners can not plan around obstacles. A global planner may rely on one or more local planners, taking the local paths they plan and connecting them to form a global path. PRP is such a global planner.
The PRP is conceptually divided into three phases: roadmap construction, roadmap refinement and query phase. PRP is incremental and all three phases can be executed multiple times and in any order. The phases are described in more detail below.
The roadmap construction phase is the heart of the PRP. During roadmap construction, the computer repeatedly generates a random configuration and tests if it is within the free space. If it is, a corresponding node is added to the roadmap and a local planner is invoked to check, if it can find a path from the new node to older nodes from the roadmap that are close to the new node. For paths that are found, edges are added to the graph. The tests are done a second time in the other direction, i.e. from older nodes in the roadmap to the new node. These second tests are not necessary, if the robot's motion capabilities are symmetrical, i.e. if for any path the reversed sequence of nodes is also a legal path for the robot. In this case the roadmap is an undirected graph.
The following pseudocode shows the algorithm used in PRPVis for the roadmap construction phase:
procedure roadmap_construction( #nodes_wanted,
n_dist,
#conn,
local_planner )
while (nodes in roadmap < #nodes_wanted)
begin
C=random robot configuration (x,y,angle);
if (robot with configuration C doesn't
collide with course)
begin
add node for C to roadmap;
CandidateNeighbours=
{roadmap node n|n ≠ C ∧ distance(n,C) ≤ n_dist};
sort CandidateNeighbours by ascending distance to C;
count = 0;
while (count < #conn ∧
CandidateNeighbours has untested nodes)
begin
n = next untested node from CandidateNeighbours;
if (local_planner can move robot from C to n)
then add connection (C,n) to roadmap;
if (local_planner can move robot from n to C)
then add connection (n,C) to roadmap;
if (made new connection) count = count + 1;
end
end
end
As can be seen, there are 4 main parameters that influence the behaviour of the algorithm:
Because the roadmap construction phase is open-ended, there needs to be an interruption condition. Here, a target value for the number of nodes in the roadmap serves to determine when the roadmap construction phase is interrupted. This target value is provided by the user.
The maximum distance that an old roadmap node may have to the newly added one in order to be considered a candidate for attempting a connection. This parameter is also user-defined.
While it would be possible to add all connections with candidate neighbours that the local planner can make, this could increase the size of the graph and slow down queries without increasing the power of the planner. Therefore, the number of connections that will be added to the roadmap is limited by #conn. Because the algorithm sorts the candidate neighbours by ascending distance from the new node, the #conn shortest connections found will be added. #conn is also controlled by the user.
The local planner is discussed in detail in a later section. Unlike the other three parameters, this one can not be set by the user in PRPVis.
The distance function and the random configuration generator could also be seen as parameters to the algorithm, but like the configuration space, to which they are closely related, they are in most cases dictated by the problem domain and fixed in an application. For that reason they are not presented as parameters in the pseudocode.
The roadmap construction phase may have created a graph that is deficient in some areas. As an example consider a narrow tunnel that connects two regions of an obstacle course that are otherwise separated by walls. The chances that a configuration picked at random from the whole configuration space will lie within that tunnel and be collision-free at the same time are small. Consequently it is very likely in this situation that the graph generated in the roadmap construction phase will consist of two sub-graphs that are not connected with each other.
The main purpose of the roadmap refinement phase is to increase the connectivity of the graph by adding new nodes in critical regions of the free space, such as the tunnel in the above example. To achieve this, the roadmap refinement phase uses a modified version of the algorithm for the roadmap construction phase. The major difference is that the candidates for adding to the roadmap are chosen in critical regions of the configuration space, rather than being picked at random from the whole configuration space. There are many different ways to do this depending on the application. In PRPVis the roadmap refinement phase leaves the choosing of candidate configurations to the user. For an interactive educational tool this is the appropriate choice.
The query phase is quite simple. It uses the roadmap generated in the construction and refinement phases to generate a path from a free configuration A to a free configuration B. This is done in a straightforward manner. Because A and B are in general not found in the roadmap, the first thing that has to be done is to find a node A' in the roadmap with the property that the local planner can find a path from A to A'. Likewise, a node B' has to be found in the roadmap from which the local planner can plan a path to B. Once A' and B' have been found, all that remains to do is to find a path N1, N2,... from A' to B' within the roadmap (e.g. using Dijkstra's shortest path algorithm). The complete path that answers the query is then obtained from the sequence of configurations A, A', N1, N2,..., B', B with the help of the local planner that returns intermediate configurations between subsequent nodes.
Finding the nodes A' and B' is the only difficulty. They are determined in a process similar to the roadmap construction algorithm. Two sets of candidate neighbours are selected, one in the vicinity of A and one in the vicinity of B. They are sorted by distance and then the local planner is invoked repeatedly to check if it can find a connection. Unlike the roadmap construction algorithm, which attempts to find #conn connections, the query algorithm can stop when the first connection is found. There is also no need to add A, B and the connections with A' and B' to the roadmap although this could be done to improve the roadmap in regions that are often used in queries.
The local planner is conceptually not a part of but rather an input parameter to the PRP in the same way that the comparison function is an input parameter to a sorting algorithm. For an application such as PRPVis, that does not solve a given motion planning problem, but merely demonstrates PRP, the local planner can be chosen freely. The choice does however influence the appearance of the program and hence the educational effectiveness. A local planner that is too dumb could result in paths that look strange, which could lead the viewer to the incorrect conclusion that PRP as a motion planning method is inadequate. If the local planner is too sophisticated, on the other hand, the viewer might not see how the generated paths are related to the roadmap and could suspect that an important mechanism is being hidden from him. Several different local planners were considered for use in PRPVis and the following was chosen because it is simple and results in paths that are easy to relate to the roadmap while still being aesthetically pleasing most of the time.
The straight line local planner used in PRPVis is applicable to the following situation:
When requested to compute intermediate configurations between configuration (x1,y1,angle1) and configuration (x2,y2,angle2), the local planner starts by rotating the robot so that its forward direction points directly at (x2,y2). Then the local planner moves the robot forward in a straight line until its reference point has reached (x2,y2). Once there, the robot will be rotated to be oriented in direction angle2. If the robot would collide with an obstacle at any point during the motion, the local planner will fail and indicate that it can not find a connection between the two configurations.
For the initial rotation to face (x2,y2) and the final rotation to assume angle2, the local planner must choose whether the rotation is done clockwise or counterclockwise. It will always choose the direction that minimizes the turning angle. If rotation into that direction fails due to a collision with an obstacle, the planner will fail, even if rotation in the other direction is possible.
This chapter will describe the program PRPVis, an interactive animation of the PRP. It is available for free download at [13]. The program is structured into a main menu and five panels dedicated to different parts of the PRP. The first two panels hold the tools to draw a 2-dimensional robot and course respectively. The remaining three panels correspond to the three phases of the PRP as they were discussed earlier. The five panels will be looked at in detail in the following sections, together with some design decisions that were made.
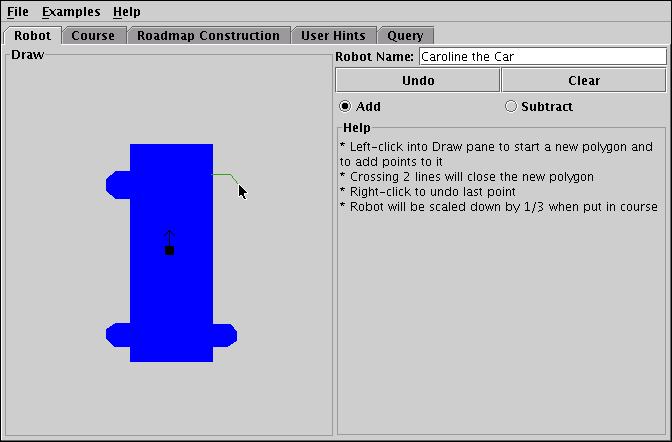
The robot construction panel which you can see in Figure 1 was kept deliberately simple. The user can edit the robot by adding or subtracting polygons specified by setting their points with the mouse. In addition to this a Clear and an Undo button are provided with obvious functionality. The view displays the robot at three times its size compared with the course view to make it easier to edit. Other than this there are no editing features, so users should be able to use the panel immediately without explanations beyond the short instructions in the Help frame. The robot name that can be entered serves no purpose other than to create a personal bond between the user and the robot he has created, and to be used as base for the suggested filename when saving the robot.
 |
| Figure 1: Drawing a car in the robot construction panel. |
The course construction panel shown in Figure 2 is almost identical to the robot construction panel and offers the same editing features. There are two noteworthy additions, though. The first is a checkbox labelled Colour difficult regions. When this box is checked, the Minkowski sum (see [14]) of the mirrored robot with the course will be computed for eight different orientations of the robot. The eight Minkowski sums will be overlayed and drawn in the course view with colouring that indicates for each point in the view how many of the eight Minkowski sum sets this point is contained in. Because the Minkowski sum of the course with the mirrored robot in a given orientation corresponds to those points where the robot is in collision with the course for that orientation, the overlaying of the Minkowski sums for different rotations gives a good approximation of the areas of the course where a randomly picked configuration is likely to be non-free. These regions are difficult for the PRP to generate roadmap nodes in and are therefore likely to require roadmap refinement to be properly covered by the roadmap. An example of a course with activated Colour difficult regions can be seen in Figure 3.
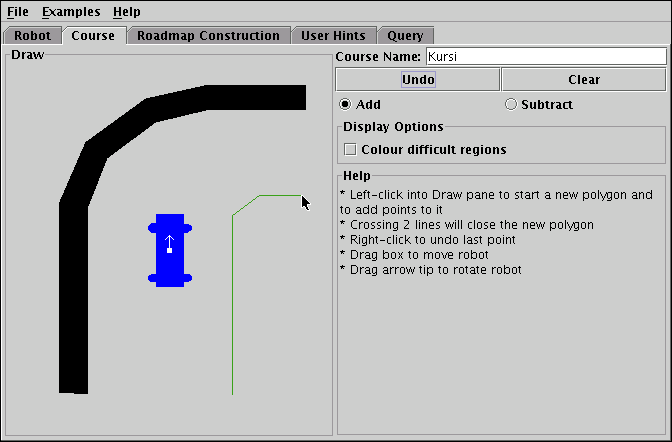 |
| Figure 2: Drawing a curve in the course construction panel. |
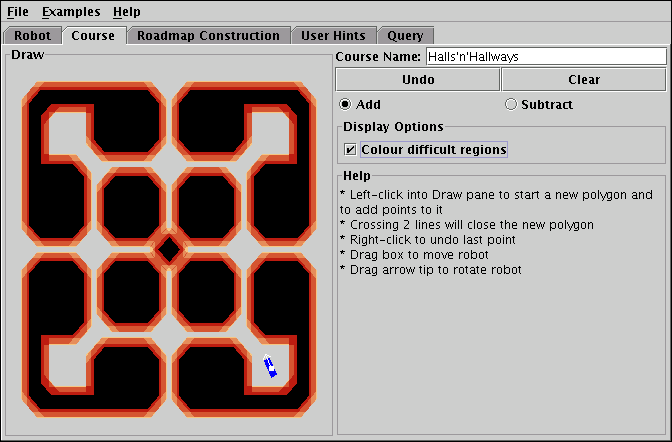 |
| Figure 3: The course Halls'n'Hallways with difficult regions for the Rectangle robot. |
The second interesting feature of the course construction panel is that the view displays an image of the robot in addition to the course. The robot's reference point and orientation are represented as a little box and an arrow attached to it. The robot image can be moved and rotated by dragging the robot's reference point and arrow tip respectively.
The purpose of the moveable robot image and the colouring of the difficult regions is to help the user dimension the course properly, i.e. to avoid creating areas that are too narrow or too wide for the robot. Both features are examples of explanatory representation. They do not play a part in the execution of the PRP algorithm and serve only to aid the user in understanding and using the program.
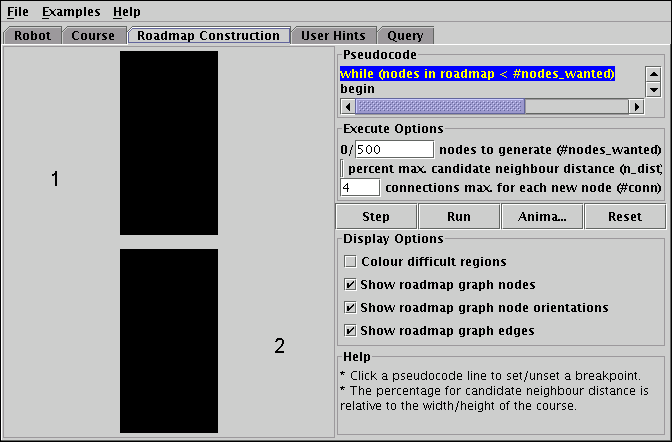
Figure 4 presents the roadmap construction panel. As mentioned in the description of the PRP, the algorithm's core part is the roadmap construction phase. So it is not surprising that this panel is the most complex of the program's five panels.
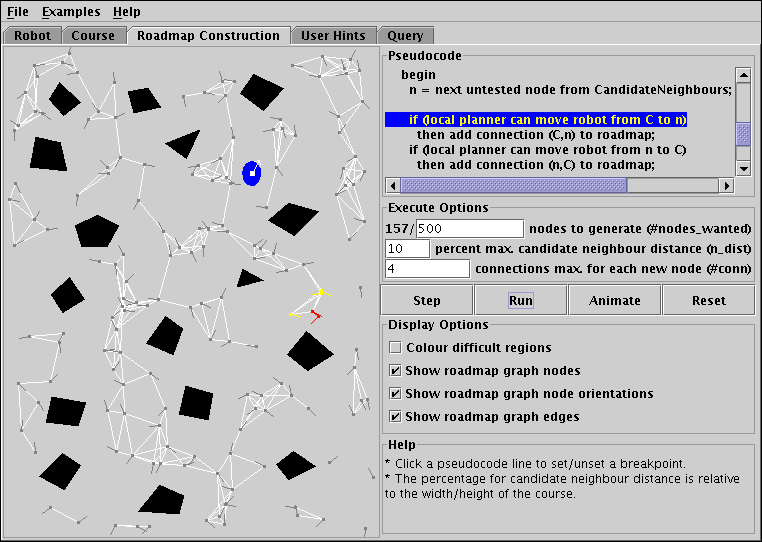 |
| Figure 4: The roadmap construction panel is the most complex of the five panels. |
The left half of the panel is taken by the data view that shows the data the algorithm operates on. In addition to the course and the moveable robot image that have already been introduced when discussing the course construction panel, the data view also displays the roadmap.
While the course construction panel has only the colouring of difficult regions as a display option, three more checkboxes have been added for the roadmap construction panel. These three checkboxes control how the roadmap is presented in the data view. The user can independently toggle the drawing of the nodes and edges of the roadmap graph. With respect to the nodes there is the choice between displaying them as small boxes with or without markers that show the orientation part of the configuration, or as orientation markers only.
In terms of abstraction, the data view operates on a very low level. Mapping nodes to boxes at appropriate locations in the course graphics, with direction indicators for the orientations, is an example of direct representation, the lowest level of abstraction possible. The lines connecting the node boxes are almost a direct representation of the edges, too. There is one important detail that has been left out, though. The roadmap graph is a directed graph, because the local planner that is being used is not symmetrical, but the directions of the edges are not shown in the data view to avoid overloading the display with details. So the edges are represented structurally but not directly. But structural representation is still a very low level of abstraction.
In cases like this, where the data structure to be drawn is an easy to grasp concept, such a low level of abstraction is appropriate. But this is only true as long as the qualitative simplicity is not overshadowed by quantitative complexity. When planning PRPVis it was not clear whether roadmap graphs with an adequate coverage of the free space would be simple enough to be drawn directly in a meaningful way. When a graph with 10000s of nodes is drawn at the resolution of a computer screen, it is next to impossible to tell apart the edges and nodes because their representations on the screen will overlap with too many others. As a solution to this problem it was planned to give PRPVis a display option for collapsing nodes that are close together, by plotting the arithmetic mean of a group of nodes rather than the individual values. This would have meant a step beyond direct and structural representation to synthesized representation of the roadmap data. But as many synthesized representations this feature would have had costs and drawbacks. The added implementation and maintenance effort required for computing the synthesized representation and keeping it in sync with the true roadmap data would have been one problem. Another problem that is more severe from an educational standpoint are the anomalies that could have resulted from the collapsed nodes view. One such anomaly would have been, for instance, the inability of the planner to find a path between two nodes that appear connected in the view. Obviously such anomalies have the potential to confuse the viewer. Fortunately it turned out that with the local planner and planning parameters that were chosen for PRPVis, graphs with few hundred nodes give adequate coverage of the free space. Such graphs are still small enough to be useful when drawn without collapsing.
The counterpart to the data view is the algorithm's pseudocode, shown in a frame to the right. The pseudocode frame is not static. The user can interact with it in several ways. One important control is the Step button that allows the user to single-step through the algorithm. A trace bar always marks the line that will be executed next. Single-stepping is not the only way to execute the code. The Animate button works like clicking the Step button repeatedly with a delay in between. It provides a way to get a slow animation of the algorithm. The Run button by contrast provides a fast animation of the algorithm, executing it as quickly as possible. The user can interrupt the animation at any time by clicking anywhere with the mouse. This is not the only way the animation may be interrupted, though. Often it is desirable to execute the algorithm only up to a certain point. The user might, for example, wish to execute the algorithm until the first time that the set of candidate neighbours is non-empty. This is easily achieved by setting a breakpoint on the first statement of the inner loop. Breakpoints are set and unset by simply clicking the line on which to set the breakpoint. Both Animate and Run will interrupt when a breakpoint is reached.
The data view and the code view are linked. In the data view nodes and/or edges that are relevant to the current line of code are highlighted in different colours to enable the viewer to establish the connection between the roadmap and the construction algorithm. This is essential for the user experience of students studying the algorithm. As the ethnomethodological experiment in [1] has shown, students feel the desire to go back and forth between the visualization and the pseudocode when studying an algorithm with the help of a visualization. This is because neither view of the algorithm is perfect. Compared to offering the pseudocode separately in other course material, the integrated side-by-side solution has the advantage that the correspondence between graphical represenation and code is at all times made clear by the trace bar and the colouring.
User interactivity is not restricted to tracing and running the code. The program allows the user to alter the values for the main parameters to the algorithm with the exception of the local planner. Playing around with the settings for #conn, n_dist and #nodes_wanted will help the user get a better feel for the algorithm and its limitations. Finally, there is the so far unmentioned Reset button. Its only purpose is to clear the roadmap and reposition the trace bar on the first statement of the code. Clearing the roadmap is necessary when one wants to experiment with a new roadmap with fewer nodes than have already been generated.
The User Hints panel shown in Figure 5 provides the user interface for PRPVis' implementation of the roadmap refinement phase. As stated earlier, the roadmap refinement phase is a modified version of the roadmap construction phase. In the case of PRPVis, the User Hints panel is a much simplified version of the Roadmap Construction panel. There is no pseudocode, because the algorithm is the same as for roadmap construction except for the fact that configurations are not randomly generated. With the pseudocode gone there is also no reason to have the animation controls, so they have been replaced with a single Hint button that executes the algorithm for the user-specified configuration. The Reset button has also been removed, because the goal was to make the User Hints panel as simple as possible, and there is no need to duplicate the Reset functionality.
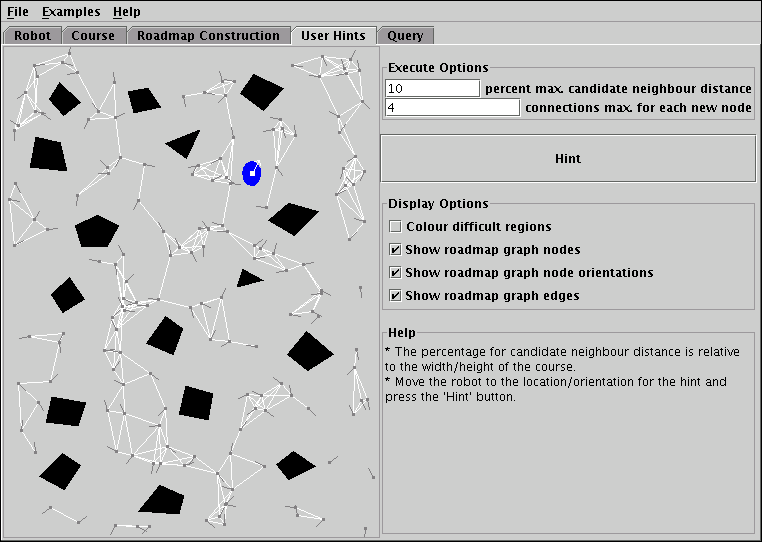 |
| Figure 5: The user hints panel is a simpler version of the roadmap construction panel. |
The educational purpose of the User Hints panel is not only to demonstrate the roadmap refinement phase. Even more important is its role in helping students comprehend the roadmap data structure that is central to the algorithm, and the difficulties of generating a roadmap that adequately covers the free space. In conjunction with the Query panel described in the next section, the students can also use the User Hints panel to test out the local planner to get a feel for the way it influences the roadmap.
The Query panel that can be seen in Figure 6 allows the user to present the program with some actual path planning problems. The left side of the panel consists of the data view familiar from the Roadmap Construction and User Hints panels, but this time it features two moveable robots. These specify the start and goal configuration respectively of the desired path. The user can position and rotate these as he pleases and when he clicks on the Animate button the planner will attempt to find a path from the configuration marked by the blue robot to the one marked by the cyan robot. If the planner is successful it will show an animation of a third robot (orange) that moves from start to goal.
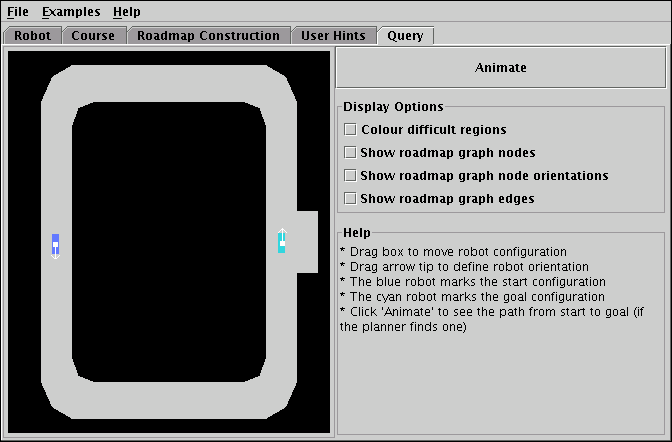 |
| Figure 6: The query panel shows a path from the blue to the cyan configuration (if found). |
Despite the Query panel's apparent simplicity, a variety of considerations guided its design, the most important issue being the scope of the animation presented to the viewer. The issue that had to be decided was the question whether pseudocode tracing should be added to the Query panel as it was done for the Roadmap Construction panel. It was decided that this would have been contrary to the educational goals of PRPVis. One problem with the code for the query phase is that it is long, because it includes finding a closest configuration in the roadmap twice, once for the start configuration and once for the goal configuration. The code for finding such a closest roadmap configuration is almost identical to the roadmap construction code but its length and the minor differences would likely lead the viewer to spend more time on the query code than the roadmap construction code. Furthermore, having two slightly different versions of the same code in PRPVis would blur the presentation of the core concepts and make them harder to learn. Another problem with the query code is the part that is concerned with finding a path within the roadmap graph. It is clearly inappropriate to include this in PRPVis, because there are several different algorithms to find such a path in a graph, such as Dijkstra's algorithm or A*, that need to be taught separately.
The problem of code length could be overcome by using a more abstract version of the pseudocode in the query panel that does not include the details on how the steps are performed and instead only lists steps such as "find node B' in roadmap graph with a connection from B' to B", but on that level of abstraction the code would raise more questions than it answers. As a consequence of these issues, it was deemed best to not have a traceable pseudocode in the Query panel. A student who has understood the concept of PRP and the roadmap construction algorithm should have no difficulties implementing the query algorithm on his own, and a student who already has problems understanding the roadmap construction algorithm should not be confronted with even more code.
The above considerations highlight the importance of the scope aspect when designing an algorithm animation. Especially when the topic of the animation includes several closely related algorithms, it is crucial to pick those parts for visualization that will benefit the understanding of the core concepts the most. The implementor of an algorithm animation may be reluctant to leave out certain details, but one must not forget that the goal of teaching an algorithm is not to get students to memorize all the intricacies of an algorithm down to the code-level, because such knowledge will not usually outlive the final examination. The primary goal of algorithm education must be to communicate the central ideas of the method.
Next to the aspect of scope, another major choice with respect to the Query panel concerned the level of abstraction at which to present the animation. An earlier version of PRPVis had the driving robot move exactly as detailed in the description of PRP's query phase, i.e. the path would contain a sequence of roadmap nodes with intermediate configurations generated by the local planner. Unfortunately, there is a problem with this approach that became very obvious when looking at the generated animation. Because the robot would always assume the exact configurations stored in the roadmap, including the orientation component, it would often rotate in one direction to achieve the correct orientation demanded by the roadmap node, only to rotate in the other direction immediately afterwards in order to face the next waypoint. The result was a motion that bore more resemblance to a windscreen wiper than to a car.
To solve this aesthetical problem, the Query panel was enhanced with path optimization as is commonly done in real world motion planning applications. A simple but effective way to eliminate the unnecessary rotations is to drop the requirement that the robot assume the correct orientation in each waypoint that it passes through. Whenever the rotation direction for facing the next waypoint would be opposite to the direction for assuming the orientation of the current waypoint, the latter will be ignored and the robot will rotate directly into the orientation to face the next waypoint. This optimization can never result in collisions because the orientations the robot goes through in the optimized path are a subset of those in the unoptimized one. Despite its simplicity, this optimization improves the quality of the generated paths dramatically.
Unfortunately, the path optimization has some drawbacks regarding the educational aspects of the program. By using optimized paths the animation's level of abstraction has been raised significantly, up to the point where an alert viewer might be confused by the fact that the robot does not travel through the exact configurations stored in the roadmap. There are several reasons why this path optimization was implemented in PRPVis despite its potential to confuse. While it might seem inappropriate to favor an approach less close to the algorithm for aesthetical reasons, the implications of using a less visually pleasing animation are severe. The viewer could get the impression that the PRP algorithm is flawed or that a much larger number of nodes is required to generate useful paths. This could diminish the motivation to study PRP. Furthermore, the unoptimized path, despite being closer to the data PRP actually delivers, could actually be more confusing to some viewers than its optimized counterpart. The reason for this assessment is that it is not immediately obvious why the robot would perform all the unnecessary rotations, especially if the direction indicators have been turned off, so that the viewer can not correlate the rotations with the data from the roadmap. Finally, it does not seem likely that the average viewer would be confused by the optimization, because it is closer to the naïve way of using a roadmap to generate a path, which is to ignore the orientation component and to simply have the robot move in straight lines from one location to the next, rotating in each waypoint to face the next. Only a viewer with a deep understanding of the subject matter would notice that it is not as simple as that. But once such a deep understanding has been attained, confusion caused by the optimization is improbable. Student feedback from actual application of PRPVis in course settings will show whether the decision to implement path optimization was beneficial to the program or not.
The main menu of PRPVis, found at the top of the screen regardless of what panel is active, consists of the three submenus File, Examples and Help. The File menu offers Load and Save functions. There are three types of file that the program can read and write: robots, courses and examples. Robot files store only the outline of the robot, course files that of the course and example files store a combination of robot and course. Example files also store the roadmap, including all automatically generated nodes as well as those added via User Hints. This is a very important property of example files, because it allows to use them as the basis for presentations that would otherwise suffer from the element of unpredictability introduced by the random number generator. The files saved by PRPVis are human-readable text files in a straightforward format. This makes it easy to use more sophisticated ways for creating robots, courses and examples if the built-in editing features are inadequate.
Because of the security restrictions of applets, the Load and Save features are not available when PRPVis is running as an applet. To compensate for this problem, the Examples menu offers some predefined robots, courses and examples that are stored directly within the applet file. The set of available examples can be customized with minimal effort.
PRPVis is not a complete courseware system to be used for self-teaching. It has been designed as supporting material for a lecture that deals with motion planning and/or probabilistic algorithms. The following sections will discuss some possibilities for using PRPVis in conjunction with a lecture. General aspects will be addressed and concrete use-cases will be given.
PRPVis can serve several purposes. It can be used as demonstration material during the lecture or it can be given to students to be used for homework, during guided lab sessions and other similar scenarios. Depending on how it is used, the students may need to be given supporting material. If students are to use the program, they will need at least a basic explanation of the PRP method, before they can begin to use PRPVis. Lecture notes or a script can provide this. If PRPVis is used as an applet, the explanation can be presented alongside the applet on the same web page. Most of the program's controls should be either self-explanatory or easy to understand by simply trying them out. The controls most likely to cause students trouble are those related to tracing the pseudocode. Students unfamiliar with debuggers will probably need a short explanation of the concept of breakpoints and single-stepping.
Concerning distribution and installation, PRPVis should pose very few problems. Because it has been implemented using the Java platform, it should be able to run without issues on every computer the students have access to, regardless of processor or operating system. Furthermore, since PRPVis can be executed as an applet that runs within the browser, it is not even necessary for students to install the program, as long as the features unsupported in applet-mode, i.e. Load and Save, are not required. This simplifies the deployment greatly as the applet can simply be put on a website accessible to students, and no further installation support has to be provided. Even if an installation as an application is unavoidable, it should not cause any trouble. PRPVis is packaged as a Java ARchive (JAR) that the Java runtime environment can execute directly. Often it will be enough for a user to download the PRPVis.jar archive and to click or double-click it in his file manager. In command line based environments the command
java -jar PRPVis.jar
executed in the proper directory should be enough to start the program. PRPVis will automatically detect whether it is being launched as an applet inside a browser or as a stand-alone application, and will act accordingly. This means that the same JAR file is used for web deployment and local installations, which avoids the problem of users downloading the wrong version and saves space on the web server.
The source code to PRPVis is conveniently provided in the same JAR file and can be extracted using the command
jar xf PRVis.jar
when the command line tools included in the Java Development Kit (see [15]) are available. With the source code it is easy to add new examples to the Examples menu and educators are encouraged to provide customized versions of PRPVis to their students. As the program is licensed under the GNU General Public License (see [16]), they may do so freely.
A lecture about algorithms can be very dry and theoretical. There are some important points that are hard to communicate. One such point that is of particular importance is the fact that the algorithm being presented works at all. This may sound surprising, but there are some algorithms for which this is not immediately obvious to everyone. Like many probabilistic methods PRP falls into this category. The idea of relying on chance for solving a problem is somewhat counterintuitive, especially when computers are concerned, which are usually associated with precise and deterministic computations. Even though few will question the fact that adding nodes at random will eventually result in a roadmap that covers the whole of free space, there will undoubtedly be skepticism regarding the practicability of this approach. After all, millions of nodes or even much more could need to be generated until a roadmap with sufficient coverage results. When confronted with a student raising this issue, there is not much a lecturer can say to counter this skepticism. This is where PRPVis can provide an invaluable help. A short demonstration that shows the generation of a few hundred nodes will give the students an impression of the practical performance of the algorithm that words or static diagrams could hardly communicate. Consequently PRPVis can save precious lecture time by replacing lengthy verbal explanations with a short animation.
But PRPVis can not only serve as a tool to answer questions and explain facts efficiently. It can also be used to raise certain questions. When the example is properly chosen, it can for instance point out interesting properties of the algorithm, such as the fact that PRP has problems with covering narrow regions of a course. When presented with the Narrow Tunnel example built into PRPVis, students will notice that PRP finds no way through the tunnel and it is likely that some student will raise this issue and it can subsequently be discussed in the lecture. This deliberate provocation of certain questions is a method to capture student attention and promote active involvement, which generally results in a better educational experience.
While PRPVis can be a useful demonstration tool when holding a lecture, PRPVis' main purpose is to be used by students. To make sure that all students use the program to the same degree it makes sense to integrate the use of PRPVis with the exercises given to students as homework or in guided lab sessions. Following are some examples for possible exercises that involve PRPVis, complete with solutions and an explanation of the exercise's purpose. The exercises are ordered by increasing level of difficulty and classified as "Basic", "Intermediate" or "Advanced".
Go to the Examples menu and select the Halls'n'Hallways example. On the Roadmap Construction panel, let the algorithm Run until it has generated 500 nodes. Now go to the Query panel and for each of the four corners 1, 2, 3 and 4 (see Figure 7) test if the planner can find a path to the hall on the opposite side of the course, marked 1', 2', 3' and 4' respectively. If no path is found, try moving start and goal configuration a little and try again. If this does not help, go back to Roadmap Construction and have the algorithm generate more nodes in increments of 100 until all four paths are found.
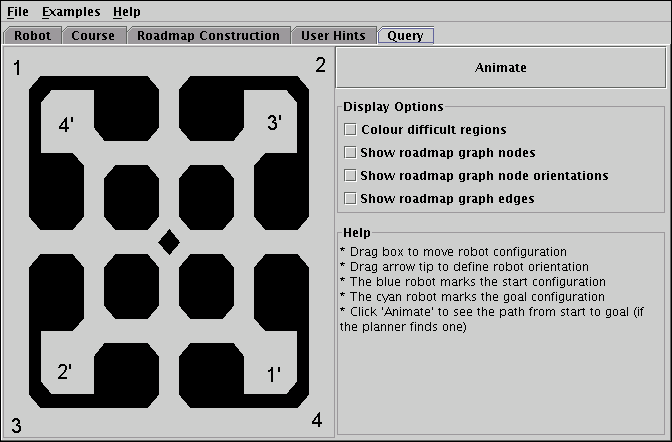 |
| Figure 7: Can the robot move from X to X' ? |
| a) |
How many nodes are needed until all four paths could be found? |
The answer to this question generally depends on the state of the random number generator when the experiment is conducted and also on the student's placement of start and goal configurations. It serves no purpose other than to get the student to play around with the different panels and get acquainted with the program. The initial 500 nodes are usually enough to connect the points.
| b) |
Select Examples/Robots/Circle to load the circular robot. Redo the experiment with this robot. How many nodes are needed this time? |
The Circle robot has more difficulties moving through Halls'n'Hallways, so 500 nodes will usually not be enough to find all four paths. Consequently this question generally forces students to play around with the control for the target number of nodes to generate. The smarter students will notice that they do not need to go back to the Query panel after each new bunch of 100 nodes has been generated, as long as the display of the roadmap edges shows that some of the halls are disconnected from the rest of the graph. When doing this exercise in a guided lab session instead of as homework, instructors should look for students who go back and forth between the Roadmap Construction and Query panels needlessly. These students might need more explanation, as it is likely they either have not completely understood the concept of finding a path within a graph, or that they are doing too much literal following of instructions and too little thinking for themselves. Thoughtless consumption is one of the major problems associated with many algorithm animations. Instructors need to ensure that students do not just look at what is happening in the graphics, but also think about why it is happening.
| c) |
Activate the Colour difficult regions checkbox and look at the resulting markings. Then load the other robot again and compare the difficult region markings for the two different robots. Generate 500 nodes again (for speed reasons turn off the Colour difficult regions before doing this and turn it on again afterwards), then count how many roadmap nodes you see inside difficult regions. Do the same for the other robot. Do your observations relate to your results for experiments a) and b)? Explain how and why. |
The areas marked as difficult for the Rectangle and the Circle robot respectively are very similar in shape, because the Circle robot covers roughly the same area as the Rectangle robot sweeps when doing a complete 360 degrees rotation around its center. This means that in a point where the Circle robot is in collision with an obstacle, there is at least one orientation in which the Rectangle robot will be in collision, too. For that reason areas that are difficult for the Circle robot are also difficult for the Rectangle robot. However, because the Rectangle robot, unlike the symmetrical Circle robot, may be able to find a collision-free orientation, the difficult regions are less difficult for the Rectangle robot.
This is clearly visible in the markings, which are dark red for the Circle robot in all places, whereas there are many orange areas for the Rectangle robot. The difficulty of the course has a direct influence on the number of roadmap nodes necessary to cover it, so from looking at the difficult regions it can be expected that there will be more nodes necessary for the Circle robot than for the Rectangle robot, which confirms the results from a) and b). The counting of roadmap nodes within difficult regions makes this even more obvious. The difficult regions for the Circle robot are all non-free, so there will be no nodes within difficult regions for it, whereas the difficult regions for the Rectangle robot contain some free configurations.
The primary purpose of this question is to acquaint students with the the Colour difficult regions option. The secondary purpose is to make them think about the issue of difficult regions and how they relate to the node generation. They should become aware of the crucial role played by difficult regions, that they can often be the most important factor that determines how many nodes are necessary to achieve complete coverage of the course and whether complete coverage is possible at all.
Load Examples/Narrow Tunnel and let the algorithm generate 500 nodes. Go to the User Hints panel and manually add nodes until the planner is able to find a path from point 1 in Figure 8 to point 2 and a path from point 2 to point 1.
 |
| Figure 8: The planner needs help to find a way through the tunnel. |
| a) |
How many nodes do you need to add? |
With the default setting of 10 for n_dist, about 10 nodes need to be added (five for each direction). This result by itself is uninteresting. It is included in the exercise only to serve as a point of reference for the following experiment and to make its result more impressive, in order to make sure that students understand that the roadmap refinement phase is not just an optimization of the PRP but a crucial step for solving many real-world problems.
| b) |
Reset the roadmap and generate 500 nodes again. Now, instead of adding nodes manually, have the program generate more nodes automatically until the planner can find paths through the tunnel in both directions. How many nodes are necessary? Why does the automatic node generation need to generate so many more nodes, although we have seen in a) that far fewer would suffice? |
The number of automatically generated nodes is several orders of magnitude higher than the 10 nodes needed in a). About 10000 nodes need to be generated automatically until the planner has made the connection through the tunnel in both directions. This should leave no doubts about the significance of the roadmap refinement step. The reason for the huge number of nodes that need to be generated before the tunnel is passable in both directions is the even distribution of the randomly generated nodes over the configuration space. The tunnel is only a very small part of the configuration space, so that it is highly unlikely that configurations will be added within it. The tunnel may not look that small in the graphics, but it must not be forgotten that the orientation is also a dimension of the configuration space. Because the robot can only pass the tunnel while oriented parallel to it, the extent of the tunnel in the orientation dimension is very small. As a consequence the tunnel is an almost 2-dimensional subset of the 3-dimensional configuration space. This is responsible for the chances of hitting it with a random configuration being so small.
| c) |
As a) and b) have shown, roadmap refinement plays a very important role when using the PRP. In real-world applications it is often unfeasible to have roadmap refinement performed manually by a human operator, so automatic refinement methods are necessary. How could the Roadmap Construction algorithm be modified to be suitable for automatic roadmap refinement? (Hint: Look at the course with Colour difficult regions checked.) |
The method for automatic roadmap refinement that this question is meant to address, is to use the roadmap construction algorithm as it is and simply replace the function that generates configurations at random, evenly distributed over the configuration space, with a function that is biased towards difficult regions, i.e. a function that has a high likelihood of generating configurations in parts of the configuration space where collisions are especially likely and that consequently need more tries to find free configurations. When looking at the markings provided by Colour difficult regions, it is immediately clear that if configurations were generated only within the area marked red, the tunnel would quickly gain more nodes without the need of trying and adding lots of unnecessary nodes in easy regions as happens in b).
Load Examples/Parking and let the program construct 1000 nodes. Go to the Query panel and place the start configuration marker at the position 1 in Figure 9 and the goal configuration marker at position 2. Make sure that the goal configuration marker's arrow points to the right. Click Animate to have the planner attempt to find a path. Now swap start and goal configuration and try Animate again.
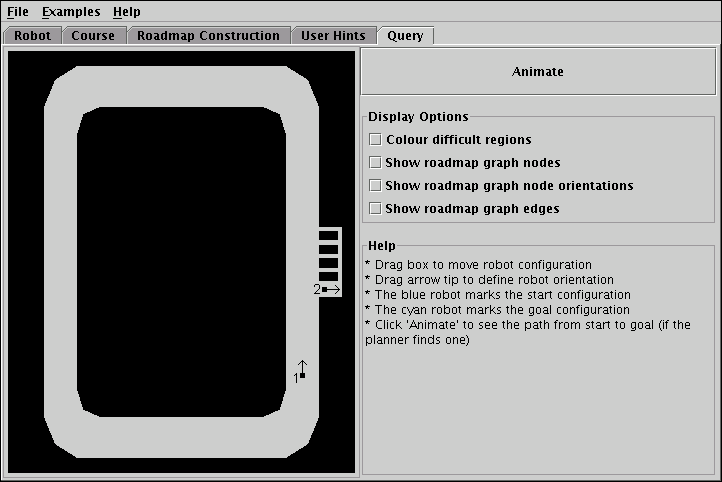 |
| Figure 9: Driving a car backwards out of a parking space is not for everyone. |
| a) |
Explain how it is possible that the planner can find a way into the parking space, but not back out again. (Hint: The roadmap graph has an important property. Which and why?) |
The goal of this question is to make the students think about the roadmap and the important fact that it is a directed graph. Furthermore, students should ask themselves why it is a directed graph. The reason is the local planner, as the following question should point out.
| b) |
Look at the Roadmap Construction pseudocode. What part(s) of the code already hint at the asymmetry problem demonstrated in a)? |
The part in question are the two if-statements in the inner loop. They clearly show that the ability of the local planner to find a connection in one direction does not imply that it will also be able to find a connection in the opposite direction. As the query phase uses essentially the same algorithm, this asymmetry manifests there, too. To prevent the planner from finding paths that move the robot into a position where it is stuck, one would either have to join these two if-statements into one if-statement (in the roadmap construction and the query code), thereby forcing the planner to return either both connections or none, or one would have to replace the local planner by a planner with the property that whenever it can move the robot from n to C it can also move the robot in the opposite direction. Note, that changing the local planner is equivalent to changing the fundamental properties of the robot.
| c) |
Assume that you are not dealing with a computer simulation but with a real robot. If you watch some path animations on the Query panel you will notice that the robot apparently has the following properties:
Look at the Roadmap Construction pseudocode again. If you were to replace the robot with one that has the additional ability of driving backwards in a straight line, would some aspect(s) of the code have to change to plan paths for the new robot? If yes, what aspect(s)? Give reasons for your answer. |
The pseudocode itself would remain as it is, but one aspect would have to be changed, namely the local planner. The local planner models the abilities of the robot. If the local planner does not match the robot's abilities, two problems can arise. The first problem is that the PRP as a whole becomes less powerful than it could be. If for instance the normal local planner from PRPVis were to be used for the enhanced robot from c), it would still suffer from the problem described in the beginning of this exercise, despite the fact that the enhanced robot could easily move from position 2 to position 1. The other, more severe problem that could arise as a result of a mismatch between local planner and robot is that the local planner reports a connection where there is none. This will result in a PRP that is unusable because it returns paths that the robot can not actually follow.
| d) |
Would using the enhanced robot from c) make a difference with respect to the problem from a) ? |
Yes, provided that the local planner is adapted to support the backwards motion of the enhanced robot, the resulting roadmap will be an undirected graph, or more precisely a directed graph where for each edge (n,C) there is a corresponding edge (C,n).
Select the example Examples/Forest of Pillars, then let the algorithm generate 500 nodes. Set n_dist to 5 and enter 600 for #nodes_wanted, but this time do not choose Run, yet. First set a breakpoint on the line "sort CandidateNeighbours by ascending distance to C;". Now click Run. The algorithm will stop at the line with the breakpoint. Count the number of candidate neighbours (shown in yellow). Repeat this five times, ignoring cases that have the node being examined very close to one of the edges of the frame. Compute the average number of candidates. In the same way determine averages for n_dist settings of 10, 15 and 20.
| a) |
What kind of mathematical relationship exists between n_dist and the number of candidate neighbours? What is the reason for this relationship? (Do more experiments if your data is not conclusive.) |
The number of candidate neighbours increases quadratically with increasing n_dist. The reason for this is that the random configurations picked by the algorithm and hence the roadmap nodes are evenly distributed across the course, so that the number of candidate neighbours is proportional to the area of the circle from which they are picked. The circle's area increases quadratically with its radius (which is n_dist). The purpose of this question is to serve as a starting point for certain complexity observations about the algorithm, namely how n_dist enters its time complexity.
| b) |
Is the relationship between n_dist and the number of candidate neighbours dependant on the course? Give reasons for your answer. |
The quadratic relationship holds for courses with few obstacles, evenly distributed over the course area, but it is not true in general. Take for instance the (degenerated) case of the long tunnel shown in Figure 10 which is just as wide as the robot. Because the roadmap is forced to become a linear, essentially one-dimensional, structure, the number of candidate neighbours only increases linearly with n_dist. For students who have not managed to come up with the reason for the quadratic relationship in the earlier question, this question may provide some help, as trying to construct a counterexample can help discover that the quadratically increasing area is responsible for the increasing number of candidate neighbours.
 |
| Figure 10: The roadmap can degenerate to a one-dimensional structure. |
| c) |
How does an increase of n_dist affect the running time of the algorithm? Does the mathematical relationship from a) also exist between n_dist and the running time? Give reasons why or why not? |
When increasing n_dist, the running time does not usually increase quadratically, although the number of iterations of the inner loop responsible for most of the running time depends on the number of candidate neighbours. The reason is the parameter #conn, whose importance this question is meant to point out. The algorithm sorts candidate neighbours by distance and the closest candidates are the most likely to result in a new connection. This means that the number of desired new connections is under most circumstances already established after processing a small fraction of the candidate neighbours, in which case the inner loop will terminate. Therefore, increasing the number of candidate neighbours by increasing n_dist will usually only add to the time needed to determine and sort the set of candidate neighbours. If the roadmap nodes are organized in a data structure such as an R-tree that eliminates the need to do a sequential scan of all nodes to find the candidates, this time is usually negligible compared to the time spent in the inner loop, because the calls to the local planner are responsible for most of the running time. It has to be noted that there are cases where increasing n_dist and consequently the number of candidate neighbours will affect the running time directly. These are cases where fewer than #conn candidate neighbours can be connected to the current configuration. In these cases all the candidate neighbours will be tested, so that an increase in the number of candidates will increase the number of iterations of the inner loop by the same amount. This can happen either because the free space is very limited and has a complex shape or because #conn has been set too high.
| d) |
Discuss the influence of the parameter #conn on the running time of the Roadmap Construction phase and the Query phase. What mathematical relationship will usually exist between #conn and the running time? |
This question is the extension of question c), taking a look at the role of #conn in more detail. As observed in c), the major role played by #conn is to limit the number of iterations of the inner loop. Increasing #conn usually has much more dramatic effects on the running time than increasing n_dist. In most situations the number of candidate neighbours is larger than reasonable values for #conn, so that increasing #conn will directly affect the number of iterations of the inner loop. The Roadmap Construction phase is not the only phase affected by #conn. In spite of the parameter not being used in the Query algorithm, it has an influence on the time taken by queries. The reason for this is simple: an increase in #conn will under most circumstances translate to a linear increase in the number of edges of the roadmap. Because the running times of common algorithms for finding paths within a graph depend on the number of edges, the time for answering a query will be adversly affected by adding more edges. Furthermore, the space requirements of the algorithm are also determined by the size of the roadmap, so adding more edges will affect the amount of memory needed, too. When discussing the answer to this question with students, instructors should point out that the additional edges in the graph only seldom improve the roadmap much, because most often they provide alternative routes only that, while they may be shorter, do not increase the overall power of the planner. Therefore the parameter #conn must be chosen with much more care than the parameter n_dist.
PRPVis in its current state of development is not very suitable for learning PRP without additional guidance through e.g. textbooks or lectures. At present, PRPVis is just a teaching aid, to supplement other course material and to be used as part of exercises. However, because of the web-embeddability of Java applets, a natural path of evolution for PRPVis would be an interactive web-based courseware to serve as a stand-alone introduction to the PRP. [10] presents guidelines for designing courseware that combines animation, text, pseudocode, semantic links and other methods to create an effective and complete learning environment. Several ideas from [10] can be easily adapted to enhance PRPVis.
The first step in such a development would be the development of a comprehensive explanation of PRP in HTML, making use of HTML's hyperlink feature together with DHTML scripting to provide terminology and other information on request and in context, rather than in a flat textbook style manner. By interfacing DHTML scripting with Java, interaction between applet and surrounding web page is possible and can be used effectively. The natural evolution path of PRPVis' tab-based approach in this context would be to split the applet into several communicating applets that focus only on specific parts of the PRP. These applets would be embedded in an appropriate explanatory context in the web page, so that the student is guided through all parts of PRP and at all times has contextually important information and interactive animation at his fingertips.